Background: Delays in care can lead to patient harm. At our large urban academic medical center, we have been struggling with increasing inpatient volumes and delays, particularly to enter our medicine, observation, and cardiology units. With a desire to provide more timely care, we used a model that employed queuing theory to predict expected delays given various levels of occupancy. This information was then used to inform decisions about the optimal number of beds needed to provide timely care.
Purpose: We tested the accuracy of a queuing theory model to estimate expected patient delays to enter a unit based on unit occupancy and help guide future bed decisions.
Description: We used a queuing theory model that was then programmed into excel to predict wait times for beds in a medicine, cardiology, and observation unit. The model was validated using actual institutional data for occupancy and wait times. Our “queue” consisted of the patients waiting for beds prior to a bed being available. Inputs included the arrival rate of patients (hourly average demand), the number of beds, average length of stay, and a discharge distribution curve based on our own institution’s data.
The model employed several assumptions: 1) the actual number of bed requests made at any hour of day is random and that the average number of bed requests depends on the time of day 2) the time each patient spends in his bed is random with a mean equal to the average length of stay 3) Decisions for discharge are made daily based on patients who are recovered prior to morning rounds 4) patients who are deemed to be ready for discharge after morning rounds don’t leave immediately but follow a distribution of discharge throughout the day.
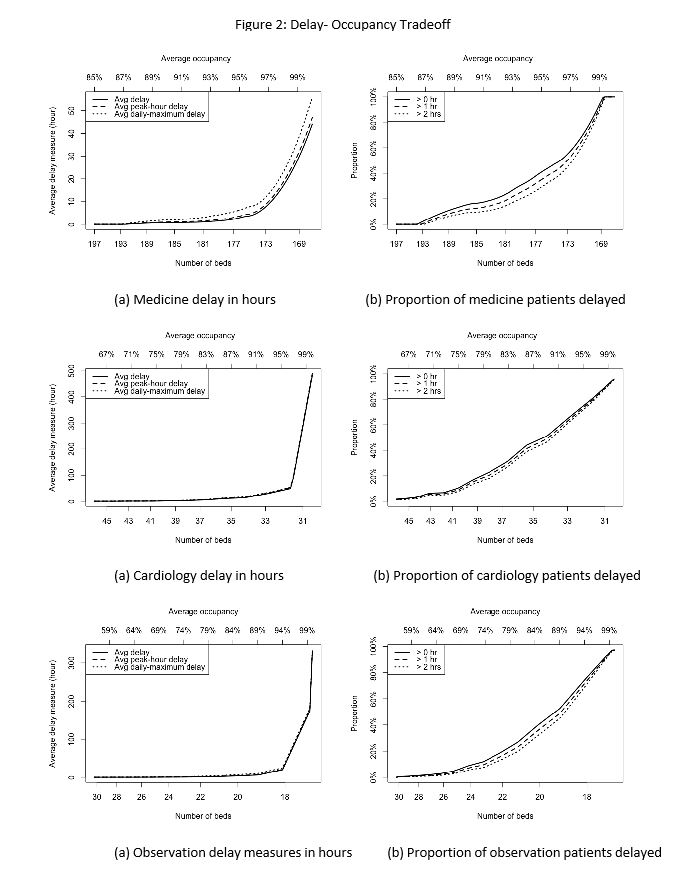
Our model closely matched actual institutional occupancy and delay data (Figure 1). As far as modeling hourly occupancy, it more closely represented actual occupancy as we found that using average occupancy (which is often used and is represented by our institutional data) underestimates actual occupancy given inaccuracies due to bed turnover at peak times . Using this model, we were able to anticipate delays based on unit occupancy for each of the 3 units (Figure 2). As predicted, wait times disproportionately increased at an accelerated rate above a certain occupancy threshold. This threshold differed between the units suggesting one size does not fit all.
Conclusions: Our model predicted average patient delays to a unit well when compared with actual data. This model can be used to guide future decisions around the optimal number of beds which would be needed for a service to meet a desired wait time goal.
.jpg)